What is TLA+?
TLA+ is a modeling language in which one can model technical systems with discrete states. It has been used to describe many things, from the jugs problem in Die Hard 3 over a diverse array of algorithms up to Amazon Storage Services. The power of TLA+ comes from the TLC Model Checker, which checks your model for certain properties. These properties could be invariants — statements that are true of every possible state, like there are no buffer overruns. And it can check temporal properties — e.g., that an algorithm eventually finishes.
TLA+ is an extremely useful tool, both for software developers as well as for many system engineers. It forces us to think first about what our system is supposed to do and to write it down in the concise and unambiguous language of math. Then we can reason about our model with the TLC model checker. And if the model is complete, we also have a specification of the system we are going to implement and that we can share with our fellow engineers.
For these reasons, I started playing around with TLA+. In this article I want to share with you how I created a working model in TLA+ step by step – including all the pitfalls and errors one can run into.
Example: A Train Siding
The easiest way to learn anything for me is to try it out myself. I wanted an example that motivates me, is simple enough so I could get quick results and was not too obvious.
I came up with an example from the railway world — as you might have noticed, I like to write about railways and how they are similar to computer networks.
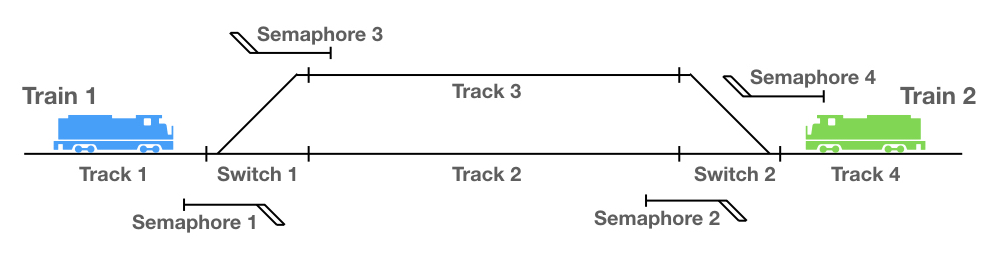
In this example, I want to model a simple train siding. This is a place on a railroad line where two trains can pass each other. One of the trains has to go first into one of the two tracks and waits there until the other train has passed. The two trains must not collide, obviously. For this reason, all tracks are protected with semaphores. Only when a semaphore shows the „go“ signal or green light may a train pass it.
This example might look trivial at first. After all, one could intuitively maneuver the trains via the siding without the possibility of a collision.
However, intuitive thinking might be enough for a model railroad, but not for a real railroad where lives are at stake. In reality, we need to make sure that the trains will never collide, even when the dispatcher who controls the switches and semaphores is a bit sleepy or distracted. So I got a hunch that even though this example may look trivial, it might prove a very interesting exercise.
Developing the Model
The first step in modeling is always to decide what to include in the model and what to exclude. I decided to focus on the simple siding, which I divided into 4 parts of tracks, track 1 to track 4, and two switches, switch 1 and switch 2. To protect all possible scenarios, I added four semaphores. This assumes that train 2 will always take track 3 and train 1 will always take track 1. They cannot choose the track to take.
I also chose to model that each train is only on one track or switch at any given moment and will never occupy two or more. In reality, this would never be the case, as a train will eventually cover at least two pieces of track or even more.
Now that we understand the problem, let’s start modeling it. You can find the TLA+ model of all steps on Github, so you can load them into the TLA Toolbox and run them yourself.
The first thing I needed to decide was which variables describe the model. The variables are the basis to formulate everything else — the invariants, the liveness properties and the actions.
I came up with this set of variables:
VARIABLES t1, t2, s1, s2, s3, s4, sw1, sw2
There are two variables for the position of the trains (t1 and t2). Four variables for the signal of each semaphore (s1 to s4). And two variables for the position of the switches (sw1 and sw2).
Note that I do not have a variable for the state of each track. I could have modeled the siding also in a way were each track keeps the information which train is currently on it, instead of having the trains remember which track they are on. But this way around it is easier to check for train collisions, so I went with it.
Next all variables need to be initialized. This happens in the action Init:
Init == /\ t1 = "TRACK1" \* Position of Train 1 /\ t2 = "TRACK4" \* Position of Train 2 /\ s1 = "STOP" \* Signal of Semaphore 1 /\ s2 = "STOP" \* Signal of Semaphore 2 /\ s3 = "STOP" \* Signal of Semaphore 3 /\ s4 = "STOP" \* Signal of Semaphore 4 /\ sw1 = "STRAIGHT" \* Direction of Switch 1 /\ sw2 = "STRAIGHT" \* Direction of Switch 2
Train 1 starts on the left side on track 1, train 2 on the opposite side. All semaphores show the STOP signal and all switches are set to the position straight.
In TLA+, it is always a good idea to add so-called Type Invariants. These are the possible values that each variable could take in any given state. If they take a value that is not listed here, the model checker will throw an error. This will protect you against mistakes in your actions and should be part of any model. My Type Invariants look like this:
Positions == {"TRACK1", "TRACK2", "TRACK3", "TRACK4", "SWITCH1", "SWITCH2"}
Signals == {"STOP", "GO"}
TypeInvariants == /\ t1 \in Positions
/\ t2 \in Positions
/\ s1 \in Signals
/\ s2 \in Signals
/\ s3 \in Signals
/\ s4 \in Signals
/\ sw1 \in {"STRAIGHT", "LEFT"}
/\ sw2 \in {"STRAIGHT", "RIGHT"}
Did you notice how I created the two sets „Positions“ and „Signals“ at the beginning so I did not have to repeat them multiple times?
OK, now that we have the basics, what is the next step? Before we go ahead and design the actions for our model, we need to think about the properties that the system should have. The most important one is a safety property: The trains must never collide! This must be true in every possible state, so it is an invariant, too. Luckily, because t1 and t2 contain the location of the trains, it is very easy to formulate this invariant:
NoCollisions == t1 /= t2
But if we only check for this property, our model would be pretty dull — a model in which the trains don’t move at all would fulfill it. This way, no goods or passengers would ever move to their destinations. So we need to formulate this goal for TLC. We want that both trains reach their destinations — track 4 for train 1, track 1 for train 2 — eventually. This makes this goal a temporal property, which can be formulated in this way:
Train1Crossed == t1 = "TRACK4"
Train2Crossed == t2 = "TRACK1"
CrossingSuccessful == <>Train1Crossed /\ <>Train2Crossed
With this temporal or liveness property we also catch situations where the trains get stuck. Checking this property will be very important as you will see later on.
The Straightforward Behavior
A complex system that works is invariably found to have evolved from a simple system that worked.
John Gall
Getting to this point was rather simple for me. But now I had to design the behavior of the system — how would the trains move, when should the semaphores change their signals, when should the switches move? I could not tackle everything at once, so I decided to begin with the simplest behavior possible: Just let the trains move in a straight line, without obeying the switches or the semaphores. This would not be realistic, but it would teach me the proper TLA+ syntax.
As the next step forward, I had to figure out how to describe this simple action: If Train 1 is on Track 1 then move it to Switch 1. Else if Train 1 is on Switch 1 then move it to Track 2. And so on. As a programmer, I intuitively tried to solve this with TLA+’s IF-THEN-ELSE construct. This even works for just two branches. But then I wanted another IF after the ELSE, which resulted in strange errors of the syntax checker. Also the CASE statement, which is similar to a switch-case in most programming languages, did not work as I expected it. Then I finally figured out the TLA+ way to do this:
\* Move Train 1 in a straight Line MoveT1 == /\ \/ /\ t1 = "TRACK1" /\ t1' = "SWITCH1" \/ /\ t1 = "SWITCH1 z /\ t1' = "TRACK2" \/ /\ t1 = "TRACK2" /\ t1' = "SWITCH2" \/ /\ t1 = "SWITCH2" /\ t1' = "TRACK4" /\ UNCHANGED <<t2, s1, s2, s3, s4, sw1, sw2>>
This has to be read like this: If t1 is equal to TRACK1 in this step, then it will be SWITCH1 in the next step. If it is SWITCH1, then it will be TRACK2, and so on. Once I wrapped my mind around this construct, it became quite natural to me. But it took me a while, I must admit.
Notice also the definition of UNCHANGED. No action is complete without the definition of the variables that do not change in this action — otherwise the model checker will complain that you have forgotten a part of the specification.
The action to move train 2 is quite similar, so I will not repeat it here. Both actions combined lead to the first specification:
\* Specification Next == MoveT1 \/ MoveT2 Spec == Init /\ [][Next]_vars
It means that the complete specification, by convention called Spec, is the combination of the initial state Init and the action Next, which describes all following states. The strange syntax with all the brackets around Next was confusing to me at first. In simple terms, it means that the specification also allows steps in which none of the variables change. This is an important property of specifications and you should add this by default, as this will allow TLC to find so-called stuttering behaviors.
How to Run the Model
Now that the first version of the specification is complete, you can run it. First, import the TLA file 01_TrainSiding_StraightLine.tla into the TLA toolbox. Then create a new model. Add the two Invariants TypeInvariants and NoCollisions under „What to Check“. Also add the property CrossingSuccessful.
Now you can run the model. These settings will be the same throughout the project, as the invariants stay the same.
After a few seconds, you should see the results. The model check found an error. The invariant „NoCollisions“ is violated. Well, that is no big surprise — in the current model both trains will move straight ahead until they collide. In the error trace you can follow the disaster step by step.

TLC shows that train 1 moved up to track 4, where it hit train 2, which had not moved. What about all the other ways in which the collision could have happened? You will not see them, as TLC stops on the first error. But having this one problem shown is enough to keep us moving.
Preventing the Disaster
After this step, we know that we have a working model which moves our trains and which detects collisions. Now we can think about how to prevent the collision. That is what semaphores are for. They protect a piece of track by denying access to it if the track is currently occupied. Let’s see what happens if the trains obey the semaphores. We add the condition to the actions for the train movement:
\* Move Train 1 in a straight Line MoveT1 == /\ \/ /\ t1 = "TRACK1" /\ s1 = "GO" /\ t1' = "SWITCH1" \/ /\ t1 = "SWITCH1" /\ t1' = "TRACK2" \/ /\ t1 = "TRACK2" /\ s2 = "GO" /\ t1' = "SWITCH2" \/ /\ t1 = "SWITCH2" /\ t1' = "TRACK4" /\ UNCHANGED <<t2, s1, s2, s3, s4, sw1, sw2>>
As we do not change the states of the semaphores in our model yet and they are initially all in the position STOP, our trains should not collide any more.
Let’s run this new model, which you find in file 02_TrainSiding_Semaphores.tla. See how the error message changes. It is no longer about the invariant NoCollisions. Instead, it reports a deadlock! A deadlock is a general condition that TLC checks. This is a situation in which the model cannot take any new steps. And TLC is right again — in this situation, neither train can move. This is a very safe state, but still now what we want. So let’s continue.
Solving the Deadlock?
Our semaphores need to get moving. This means we have to have a few actions that will move them to a new signal, like this:
ChangeS1 == /\ t1 = "TRACK1"
/\ t2 \notin {"TRACK2", "SWITCH1"}
/\ sw1 = "STRAIGHT"
/\ s1' = "GO"
/\ UNCHANGED <<t1, t2, s2, s3, s4, sw1, sw2>>
What are the conditions here? The first checks that train 1 is waiting in front of the semaphore 1. It should not switch just by itself when it is not needed. The next condition is that the other train is not on the track that train 1 wants to enter, to prevent a collision. And the last condition is that the switch is leading to that track. All pretty straightforward.
The conditions for the other semaphores look similar. You can find the complete code in 03_TrainSiding_ChangingSemaphores.tla. There I also added just another action, which changes the state of switch 1:
\* Change switch 1 ChangeSw1 == /\ \/ /\ sw1 = "STRAIGHT" /\ sw1' = "LEFT" \/ /\ sw1 = "LEFT" /\ sw1' = "STRAIGHT" /\ UNCHANGED <<t1, t2, s1, s2, s3, s4, sw2>>
I did this so the trains have a chance of crossing each other.
With all these additional actions, the Next action looks much bigger:
Next == MoveT1 \/ MoveT2 \/ ChangeS1 \/ ChangeS2 \/ ChangeS3 \/ ChangeS4 \/ ChangeSw1
You might ask yourself: How do we synchronize all these different actions with each other? How do we make sure that we first change the switch, then the semaphore, and then the train?
Well, we don’t. This specification allows each step to happen at any time in principle, and this is what we want. After all, our goal is to check all possible combinations for errors, even the very unlikely ones. TLC does not care about probabilities, only for possibilities. And this allows us to build reliable systems: To find also the corner cases that happen rarely, but can have disastrous consequences.
What do you think will happen when you run this model? Will it fulfill all our desired properties now that a switch and the semaphores can change their states too?
Well, actually it can’t, as I forgot to change the next state actions for the train movement. They will never follow the switch to the siding, as they do not check for the switch state. So the model is incomplete. I expected a deadlock again, as the two trains would be stuck again at a semaphore. But what I got was quite a different error:
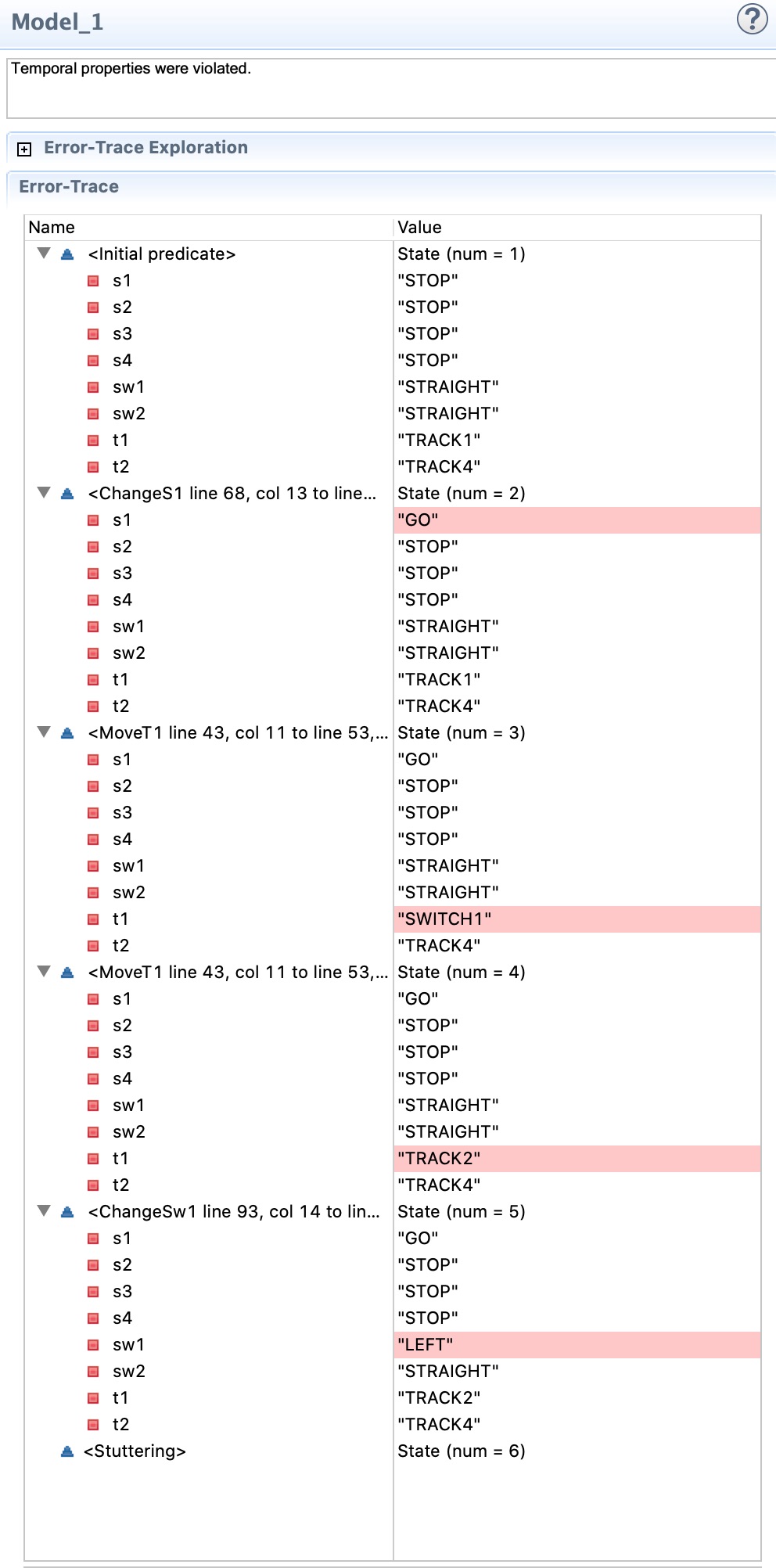
It says: Temporal properties were violated. Hm, what does this mean. A look into the stack trace gives a clue: It ends with a stuttering step. A what?
Let’s have a look at the second-to-last step, step 5. Train 1 has progressed to track 2, but is now stuck at semaphore 4, as train 2 is still in its original position and can also not leave as it will not follow switch 2 to the siding.
But the model did not stop there. Instead, it switched switch 1 to the LEFT state. This is the only action still enabled in this situation, so the model can continuously do this step. It switches between LEFT and STRAIGHT. On and on and on. Actually we have reached a deadlock, just one were one part of the model keeps busy. But no problem, we now how to solve this one, don’t we?
Overcoming Stuttering
The stuttering occurred because our trains did not follow the switches yet. So all we need to do now is to change the actions for the trains accordingly. First, I added the action to change switch 2, which you find in 04_TrainSiding_ChangingBothSwitches.tla. But the real deal comes in 05_TrainSiding_MovingTrain2OverSiding.tla. Here train 2 will follow the switches, like this:
\* Move Train 2 via the siding MoveT2 == /\ \/ /\ t2 = "TRACK4" /\ s4 = "GO" /\ t2' = "SWITCH2" \/ /\ t2 = "SWITCH2" /\ t2' = IF sw2 = "STRAIGHT" THEN "TRACK2" ELSE "TRACK3" \/ /\ t2 = "TRACK2" /\ t2' = "SWITCH1" \/ /\ t2 = "TRACK3" /\ s3 = "GO" /\ t2' = "SWITCH1" \/ /\ t2 = "SWITCH1" /\ t2' = "TRACK1" /\ UNCHANGED <<t1, s1, s2, s3, s4, sw1, sw2>>
Well, this should do it. The trains can pass each other now and every track is protected by semaphores. Just one more run of the model checker to be sure:
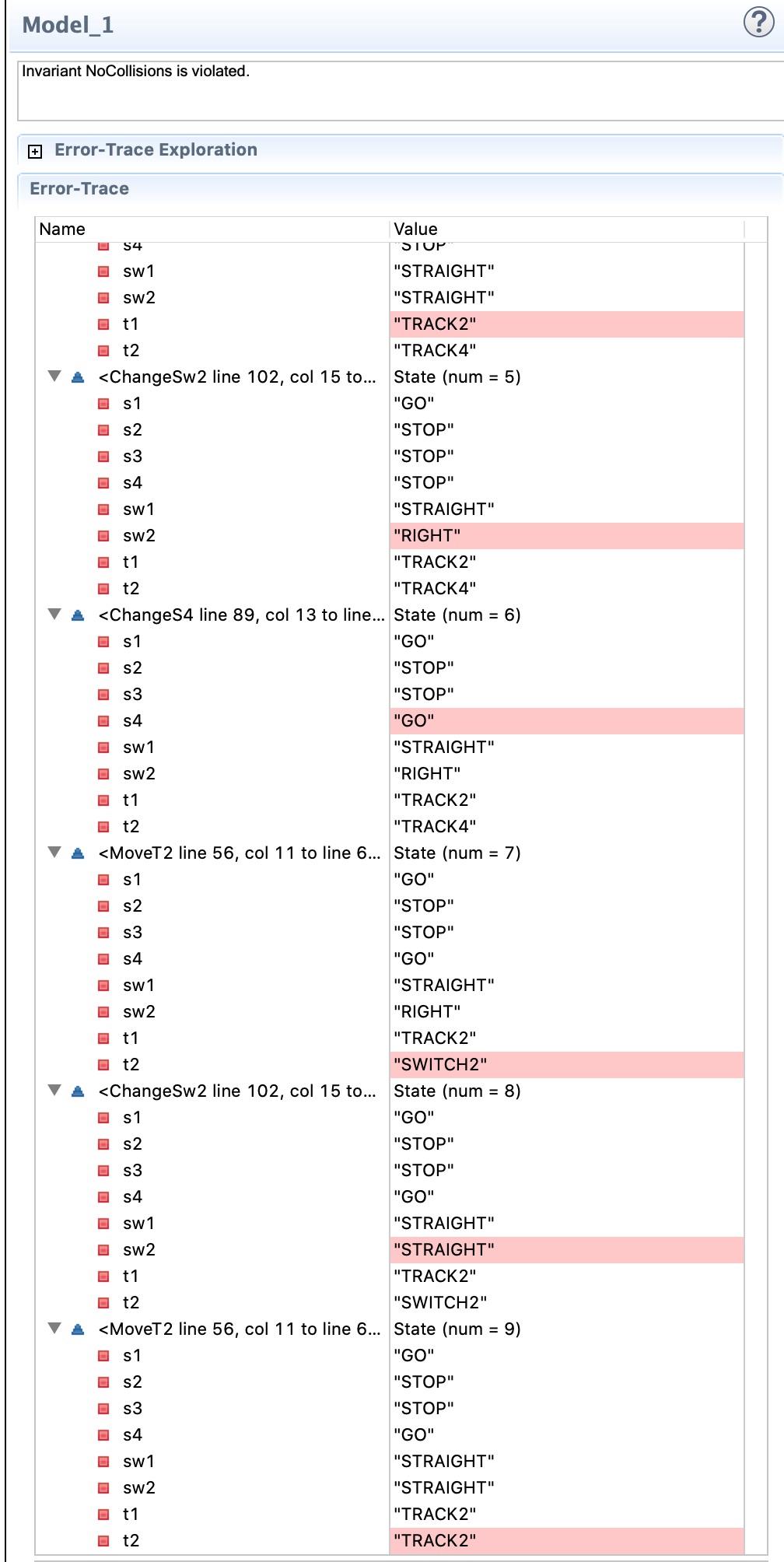
Oh, what is this? There is a collision! There must have been something that I have overlooked. Let’s check the error trace:
So, train 1 proceeds to track 2 and stops at semaphore 2. Looks good so far. Then switch 2 changes to the RIGHT position, semaphore 4 goes to green and train 2 proceeds to switch 2. All good so far. But then the disaster happens: Switch 2 changes to the STRAIGHT position while train 2 is right on top of it. Then train 2 will continue straight ahead and crash into train 1.
It turns out our model has failed to fulfill one of the basic requirements of real-life interlockings: Once a semaphore turns to GO, the switches on the train’s path must not be changed until the train has passed this section of track.
Looks like I am not done at all, and TLC has saved me from designing a potentially dangerous system.
Avoiding the Crash — Once More
The specification in 06_TrainSiding_ProtectingSwitches.tla fixes the problem we found in the last step. I added a check to the actions that change the switches. They must only change when the corresponding semaphores say STOP. If one of them is showing a green light, the semaphore will not switch states:
ChangeSw1 == /\ s1 = "STOP" /\ s3 = "STOP" /\ \/ /\ sw1 = "STRAIGHT" /\ sw1' = "LEFT" \/ /\ sw1 = "LEFT" /\ sw1' = "STRAIGHT" /\ UNCHANGED <<t1, t2, s1, s2, s3, s4, sw2>>
The crash is finally fixed!
Can the trains pass each other now?
I hoped it were all done now — but when I ran the model again, there was another error. The crash is fixed, but a deadlock was detected. What happened?
In the last state, the trains were standing on track 2 and 3, right next to each other. So far, so good. But semaphores 1 and 4 were on GO. With the rules just introduced, the switches must not change in this situation, so the trains cannot continue. What was I missing now?
Resetting the Semaphores
Well, I ignored one of the other important rules for interlockings, and TLC reminded me of it. The semaphores that the train pass are never reset to STOP. This means the track section that the train just entered is not protected against trains that follow this train. This must not happen!
In real life, the requirement is that a semaphore switches to STOP once a train has passed it. Our model does not yet do this. I added it by extending the action of the trains: Whenever they passed a semaphore, the semaphore switches back to STOP.
MoveT1 == /\ \/ /\ t1 = "TRACK1" /\ s1 = "GO" /\ t1' = "SWITCH1" /\ s1' = "STOP" \* Change semaphore to STOP once the train has passed it /\ UNCHANGED s2 \/ /\ t1 = "SWITCH1" /\ t1' = "TRACK2" /\ UNCHANGED <<s1, s2>> \/ /\ t1 = "TRACK2" /\ s2 = "GO" /\ t1' = "SWITCH2" /\ UNCHANGED <<s1>> /\ s2' = "STOP" \/ /\ t1 = "SWITCH2" /\ t1' = "TRACK4" /\ UNCHANGED <<s1, s2>> /\ UNCHANGED <<t2, s3, s4, sw1, sw2>>
You can find this change in 07_TrainSiding_ResettingSemaphores.tla. It also adds the check that a switch most not be changed while a train is currently on it, which would also be possible otherwise.
In reality, both checks are done by employing track occupancy detectors and axle counters that can detect when a train enters or leaves a certain section of the track.
However, this is still not the final model. The deadlock is fixed, but it shows another stuttering behavior. Here, train 2 is already on track 1, but train 1 is stuck on switch 2. What happened? There is no semaphore blocking train 1.
It turns out that the specification allows for a behavior where switch 1 just keeps changing its state all the time, without train 1 ever taking its last step forward. This happens because of a property that is missing in our spec — fairness.
Being Fair to the Trains
By default, if an action is enabled in TLA+, it might happen — but it might as well not happen at all. This is very useful to check how a system behaves if a certain thing that is expected never occurs — like a message never being received. In our case, we are not interested in what happens if a train stops moving. Maybe the engine broke down, or there was a blockage on the tracks. Whatever it is, our model is not concerned with this kind of thing because this is a situation that cannot be handled by automated systems in reality. In such a case, the train needs human intervention to get it moving again. Until then, every train movement on this line is blocked.
OK, but what do we do then so that our model assumes every step that can be taken will eventually be taken? This can be done by adding weak fairness to an action. This tells TLA+ that this action should eventually be taken, so our trains will not get stuck. We do this as part of our Spec:
Spec == Init /\ [][Next]_vars /\ WF_vars(MoveT1) /\ WF_vars(MoveT2) /\ WF_vars(ChangeS1) /\ WF_vars(ChangeS2) /\ WF_vars(ChangeS3) /\ WF_vars(ChangeS4) /\ WF_vars(ChangeSw1) /\ WF_vars(ChangeSw2)
I added weak fairness to each action, as I think none of them should ever get stuck for the sake of our model, consciously ignoring the fact that each of these parts of the system might fail in reality. You can find this new definition in 08_TrainSiding_Fairness.tla.
Let’s see what this does to the result of the model check. We get a deadlock again! What is the error now? Let’s see. Hm, train 1 is on track 4. Train 2 is on track 1. That is our goal, and it was reached! Finally!
But why this error message? It turns out that our model only describes the steps up to this point. Once the trains have reached their destinations, they will not move any more. Nothing happens at all. A classical deadlock.
I don’t want to extend the model to let the trains go on and on and on, because we would never finish this exercise. So I decide to remove the check for the deadlock so hopefully no other error will be found…
Not quite yet. TLC reports another stuttering step. Here train 2 advances up to track 3 and train 1 is still on track 1. Instead of train one progressing, switch 1 keeps changing its state forever. Seems like the dispatcher in our interlocking can’t make up his mind.
Finishing the Model — Now for Real
Spoiler alarm: This is really the last step to fulfill all our checks.
In this step, I added a rule how to decide the priority if two trains are waiting to pass the same switch. The rule is simple: If train 1 is waiting, it must pass first, otherwise the track will never become free. To a human dispatcher, this rule is obvious, but not to the computer. So let’s extend our action for switch 1:
ChangeSw1 == /\ s1 = "STOP"
/\ s3 = "STOP"
/\ t1 /= "SWITCH1"
/\ t2 /= "SWITCH1"
/\ \/ /\ sw1 = "STRAIGHT"
/\ t2 = "TRACK3"
/\ t1 /= "TRACK1" * Only change switch one once track 1 is free
/\ sw1' = "LEFT"
\/ /\ sw1 = "LEFT"
/\ t1 = "TRACK1"
/\ sw1' = "STRAIGHT"
/\ UNCHANGED <>
This change finally reports no errors at all. The model has 91 states, of which 44 are distinct. In the end, all steps lead to the trains passing each other without crashing. We are done!
You can find this last version of the model in file 09_TrainSiding_ConflictResolution.tla.
Conclusion
When I started with this example, I wanted to do something simple enough that I could finish it in a short time, but still complex enough to teach me something interesting.
I finished the example on a weekend, but it took me more time than expected. I thought I understood the problem situation well, but TLC found many problems in the model that I would never have spotted myself. This was a very valuable lesson for me. Even though a problem seems simple, there might be hidden details. By modeling the system or the software ahead of building it, we can find many problems that would have shown up only much later in the process.
Limitations
As it is the nature of a model, it cannot include all details of reality. I had to do some simplifications. For instance, the trains in my model only occupy one piece of track at a time. In reality, trains have a certain length and they will at least temporarily occupy two or even three pieces of track, e.g. when they pass a switch.
Also the equipment never breaks down in the model, which it very well does in reality. If we wanted to model this behavior, we would need a much more sophisticated model. We would need to define all failures modes of each piece of equipment and what to do in reaction to it. Then we need to check if this extended description still fulfills the high-level model we have constructed in this example. TLA+ supports this kind of multi-layered description of models through refinements. If you have the need for such an extended model, you can dig deeper into this topic.
This was the first real project I did all by myself in TLA+. As such, I tried to use only the most basic language constructs not to confuse myself. There are many more things one could use in specifications, such as tuples, functions or external modules. These might be part of a future example.
How to Write a Model
Working on this model, I developed an understanding of the general process of modeling in TLA+. The first thing to do is to think about the variables that describe the system. These are the basis for all the other parts of the model: For the invariants and temporal properties as well as for the actions. All of them operate on these variables.
Once you have decided on the variables, you can describe the temporal properties and the invariants. It is always helpful to include a type invariant, that will check that you did not assign a value to a variable that is not allowed. Once you have created these properties, you can add them to the model check and start running the model. Running the model early and often helps to find errors quickly, before you have gone in the wrong direction for too long.
When all of this is in place, the actions can be formulated. It is helpful to start with the simplest thing that you can do and then check which invariants are violated. Ideally, you have a clear expectation of the result at this step, so that you can validate your expectation with the result of the model check. If the system behaves differently, go one step back and think about what causes the different behavior. This might teach you something about TLA+ or about your system.
Then you can grow your system from a very simple behavior to a more and more sophisticated one, running the model check in each step to guide your development process.
Once all checks are passed, you are done for now and can decide what to do with the result.
Maybe you will use it as a specification for a piece of software that you are gonna write. Maybe you have just jotted done a few ideas about the system and now you want to discuss them with a colleague. Or you want to dig deeper and refine the model, to come even closer to reality.
Reading and Readability
While writing the specification, I also made a few mental notes about how to read a specification somebody else has written.
Due to the syntax of TLA+, all specifications have a similar structure. The variables have to go on the top, the description of Spec and Next on the bottom and the actions in between.
An action has to be declared first before it can be used by another action, so if you read from top to bottom, you will see the details first before you get the big picture.
It is much easier to read the other way round. Once you have read the declaration of the variables, jump to the bottom to the definition of Spec and Next. Then work your way upwards through the actions. This way, you can build up an understanding of the whole specification step by step.
When reading a specification, it might be easier to use the pretty-printed PDF version that the TLA+ toolbox can create. This replaces the ASCII representation of the mathematical symbols with the actual mathematical symbols and thus is a bit easier to read.
There are also a few things you can do to improve the readability of your own spec:
Use sections, which separate the different parts of your spec from each other. This makes it easier to spot, e.g. where the definition of the invariants ends and where the actions start.
A section is created by adding a line with at least four dashes.
Assign meaningful names to your variables. As in programming, try to avoid names like x or var, which don’t have any meaning by themselves.
Try to assign a name to each construct in your program. As you can see, I have given the conditions that TLC checks names like CrossingSuccessful. There is no technical reason, as I could have configured the model check to check for <>Train1Crossed /\ <>Train2Crossed instead of CrossingSuccessful. For the program, it makes no difference, but for the readers of the spec it does.
Outlook
By building this relatively simple example, I learned a lot about TLA+ and I feel prepared to write more sophisticated specifications and explore the other constructs of TLA+.
I hope you learned something while following my experiment. As with all tools, the best way to learn them is to use them. I would be very happy if this example inspired you to try out TLA+ with your own ideas.